Greatest Common Factor Of 36
Factors of 36
Factors of 36 are those numbers that divide 36 completely without leaving any remainder. There are 9 factors of 36 among which 36 is the biggest factor and 2 and 3 are its prime number factors. The prime factorization of 36 can be done by multiplying all its prime factors such that the product is 36. Let us learn about all factors of 36, the prime factorization of 36, and the factor tree of 36 in this article.
| 1. | What are the Factors of 36? |
| 2. | Prime number Factorization of 36 |
| 3. | Factor Tree of 36 |
| iv. | Factors of 36 in Pairs |
| five. | FAQs on Factors of 36 |
What are the Factors of 36?
The factors of 36 can be listed as 1, ii, 3, iv, 6, ix, 12, eighteen, and 36. Co-ordinate to the definition of factors, the factors of 36 are those numbers that divide 36 without leaving any remainder. In other words, we tin say if two numbers are multiplied and the product is 36, and so the numbers are the factors of 36. It means that 36 is completely divisible by all these numbers. Apart from these, 36 also has negative factors that can be listed equally, -1, -2, -3, -4, -6, -9, -12, -18, and -36. For negative factors, we demand to multiply a negative factor past a negative cistron, like, (-12) × (-3) = 36.
How to Find the Factors of 36?
Factorization of a number means writing the number every bit a production of its factors. The most ordinarily used method to find the factors of a number is using the multiplication method. Let u.s.a. find the factors of 36 using multiplication.
Factors of 36 using Multiplication
Let us find the factors of 36 using the multiplication method using the following steps.
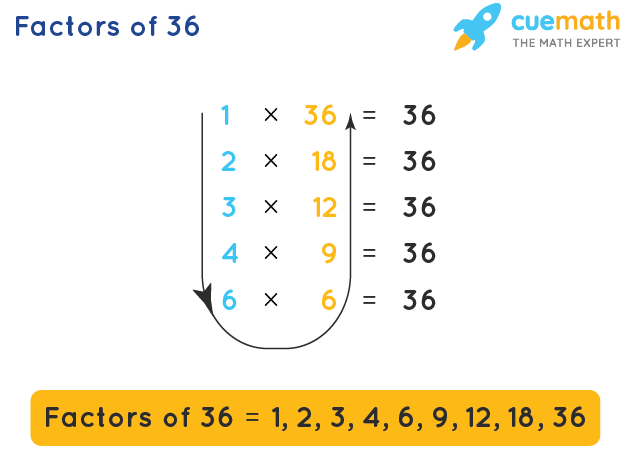
- Step one: In order to observe the factors of 36 using multiplication, we demand to check what pairs of numbers multiply to get 36, and so we demand to split up 36 past natural numbers starting from ane and go on till 9. We need to brand a note of those numbers that separate 36 completely.
- Step 2: The numbers that completely divide 36 are known as its factors. Nosotros write that particular number forth with its pair and make a list as shown in the effigy given above. As we check and list all the numbers upward to nine, we automatically become the other pair factor along with information technology. For example, starting from i, we write 1 × 36 = 36, and 2 × eighteen = 36 and and then on. Here, (1, 36) forms the start pair, (2, 18) forms the second pair and the list goes on as shown. And so, as we write i as the factor of 36, we get the other gene equally 36; and as we write 2 every bit the factor of 36, we go 18 as the other gene. Like this, nosotros get all the factors.
- Step three: Later on the listing is noted, nosotros go all the factors of 36 starting from one up there, coming downwards and then nosotros go upward once again up to 36. This gives us a complete list of all the factors of 36 equally shown in the figure given above.
Therefore, the factors of 36 tin be listed as i, two, 3, four, 6, 9, 12, 18, and 36. Now, allow us learn nearly the prime factorization of 36.
Prime Factorization of 36
Prime factorization is a way of expressing a number every bit a product of its prime factors. The prime factors of a number are those factors that are prime numbers. The prime factorization of 36 tin exist done using the following steps. Detect the effigy given below to empathize the prime factorization of 36.

- Step 1: The first step is to divide the number 36 with its smallest prime factor. We know that a prime number factor is a prime which is a factor of the given number. So, with the help of divisibility rules, we notice out the smallest factor of the given number. Here, nosotros go 2. Therefore, 2 is the smallest prime gene of 36. Then, 36 ÷ 2 = xviii
- Step 2: We demand to repeatedly split the quotient by 2 until we get a number that is no more divisible by two. And then, nosotros split up 18 once more by ii which is eighteen ÷ two = 9
- Step three: Divide eighteen again by two which results in 18 ÷ 2 = 9
- Stride 4: Now, 9 is not completely divisible past 2, so, we keep with the adjacent prime number factor of 36, which is 3. That is nine ÷ 3 = 3
- Stride 5: Split up the quotient by three once again which is iii ÷ 3 = i
- Pace vi: We demand non proceed further as we have obtained 1 equally our quotient.
- Step 7: Therefore, the prime factorization of 36 is expressed as 2 × two × 3 × 3 = 22 × iii2; where 2 and iii are prime numbers and the prime factors of 36.
Therefore, the prime number factors of 36 are 2 and 3 and the Prime factorization of 36 = 2 × 2 × 3 × 3
Gene Tree of 36
We can also observe the prime factors of 36 using a cistron tree. The factor tree of 36 can exist drawn by factorizing 36 until nosotros reach its prime factors. These factors are divide and written in the form of the branches of a tree. The final factors are circled and are considered to exist the prime factors of the 36. Let us find the prime factors of 36 using the following steps and the cistron tree given below.

- Footstep 1: Split 36 into 2 factors. Let usa have two and 18.
- Stride 2: Discover these factors to see if they are prime number or not.
- Step 3: Since 2 is a prime we circumvolve information technology as 1 of the prime number factors of 36. We motility on to 18, which is a composite number and farther divide it into more factors. In other words, we echo the procedure of factorizing 18 and splitting information technology into branches until we reach a prime number.
- Step four: Hither, we get 2 and 9. So, we circumvolve 2 considering it is a prime number and we split 9 into three and 3. At this stage, we are left with prime numbers, 2 and iii. We circumvolve them since we know that they cannot be factorized further. This is the end of the factor tree.
- Footstep v: Therefore, the prime number factors of 36 = 2 × 2 × 3 × three
Note: It should be noted that there can be different gene trees of 36. For instance, we tin start by splitting 36 into 4 and 9. Then, 4 can be split farther into 2 and two, while 9 can be divide into 3 and iii. Finally, we can detect the same prime factors, that is, 36 = 2 × 2 × three × iii
Factors of 36 in Pairs
The factors of 36 tin be written in pairs. This means that the production of the pair factors of 36 is always 36.The factors of 36 in pairs tin be written as shown in the table given below:
| Factors | Positive Pair Factors |
| ane × 36 = 36 | i, 36 |
| 2 × 18 = 36 | ii, 18 |
| iii × 12 = 36 | 3, 12 |
| iv × 9 = 36 | 4, 9 |
| vi × half-dozen = 36 | 6, 6 |
It is possible to have negative pair factors as well because the product of 2 negative numbers as well gives a positive number. Let united states have a wait at the negative pair factors of 36.
| Factors | Negative Pair Factors |
| -1 × -36 = 36 | -one, -36 |
| -2 × -18 = 36 | -2, -18 |
| -3 × -12 = 36 | -3, -12 |
| -iv × -9 = 36 | -four, -9 |
| -6 × -6 = 36 | -6, -half dozen |
The following points explain some features of the pair factors of 36.
- The pair factors of the number 36 are whole numbers in pairs that are multiplied to get the original number, i.eastward., 36.
- Pair factors could exist either positive or negative merely they cannot be fractions or decimal numbers.
- The positive pair factors of 36 are equally follows: (ane, 36), (2, eighteen), (three, 12), (4, nine), and (6, 6). The negative pair factors of 36 are (-one, -36), (-ii, -18), (-3, -12), (-4, -9) and (-half-dozen, -6)
Important Notes
- Only composite numbers tin can accept more than than ii factors. Since 36 is a composite number, it has more than two factors.
- Every cistron of a given number is either less than or equal to the given number.
- The number of factors of a given number is finite. 36 has ix factors.
- Factors of 36 are those numbers that divide 36 completely without leaving any rest.
- 36 has a total of 9 factors: 1, 2, three, iv, 6, 9, 12, xviii, and 36.
- There is a fox to calculate the total number of factors of a number. For case, 36 = 2 × 2 × 3 × three = 22 × 3ii. We get the prime number factorizations of 36 as 2two × 32. Just add together 1 (i) to the exponents ii and ii individually and multiply their sums. (ii + ane) × (two + 1) = 3 × 3 = ix. This ways 36 has 9 factors in all.
Points to retrieve
Let us recollect the list of the factors, the negative factors, and the prime factors of 36.
- Factors of 36: 1, 2, three, 4, 6, nine, 12, 24, and 36.
- Negative Factors of 36: -1, -2, -3, -4, -half-dozen, -9, -12, -18, and -36.
- Prime Factors of 36: 2, 3
- Prime number Factorization of 36: 2 × two × 3 × 3 = 2ii × 3ii
☛ Related Manufactures
- Factors of 33: The factors of 33 are 1, three, 11, and 33.
- Factors of 34: The factors of 34 are 1, 2, 17, and 34.
- Factors of 38: The factors of 38 are 1, 2, nineteen, and 38.
- Factors of 30: The factors of 30 are i, 2, three, 5, vi, ten, fifteen, and 30.
- Factors of 360: The factors of 360 are 1, two, 3, 4, 5, six, 8, ix, x, 12, 15, eighteen, 20, 24, thirty, 36, 40, 45, 60, 72, ninety, 120, 180, and 360.
- Factors of 35: The factors of 35 are 1, 5, 7, and 35.
- Factors of 37: The factors of 37 are 1 and 37.
Examples on Factors of 36
become to slidego to slidego to slide

Break down tough concepts through simple visuals.
Math will no longer be a tough subject, particularly when you lot understand the concepts through visualizations.
Book a Costless Trial Class
Do Questions on Factors of 36
go to slidego to slide
FAQs on Factors of 36
What are the Factors of 36?
The factors of 36 are one, 2, 3, 4, 6, 9, 12, 18, 36 and its negative factors are -1, -ii, -iii, -4, -half dozen, -9, -12, -xviii, -36.
What are the Prime Factors of 36?
In that location are two prime number factors of 36, and they are ii and iii. The prime number factors of a number are those factors that are prime numbers. In this case, if nosotros do the prime factorization of 36, we get 2 × 2 × 3 × iii = 22 × 32, where two and 3 are prime number numbers and the prime number factors of 36.
What are the Mutual Factors of 36 and 42?
The factors of 36 can be listed equally 1, two, 3, 4, vi, 9, 12, 18, 36 and the factors of 42 can be listed equally 1, 2, three, six, 7, fourteen, 21, 42. Among these, we can list the mutual factors of 36 and 42 as 1, 2, 3, and half-dozen. At present, we can notice the Greatest Common Cistron (GCF) of 36 and 42 which is six.
What are the Common Factors of 36 and 40?
The factors of 36 can be listed as 1, two, 3, 4, 6, 9, 12, eighteen, 36 and the factors of forty tin be listed as i, two, 4, 5, 8, 10, twenty, 40. Among these, we tin can listing the common factors of 36 and 40 equally ane, 2, and 4. With the assistance of this, we can detect the Greatest Common Factor (GCF) of 36 and 40 which is 4.
What is the Greatest Common Gene of 36 and 20?
The factors of 36 and 20 are 1, 2, three, 4, 6, 9, 12, 18, 36 and ane, 2, 4, 5, 10, twenty respectively. The Common factors of 36 and twenty are (1, two, four). Hence, the GCF of 36 and 20 is four.
What is the Sum of all the Factors of 36?
The sum of all the factors of 36 can be calculated by adding one, 2, 3, iv, 6, 9, 12, 18, 36 which is 1 + 2 + 3 + 4 + 6 + 9 + 12 + 18 + 36 = 91.
Greatest Common Factor Of 36,
Source: https://www.cuemath.com/numbers/factors-of-36/
Posted by: eppersonhisdon.blogspot.com


0 Response to "Greatest Common Factor Of 36"
Post a Comment