Percent Ionization Of Weak Acid

sixteen.half dozen: Weak Acids

Terminal updated
Salvage equally PDF

Page ID: 25230

Learning Objectives

Assess the relative strengths of acids and bases according to their ionization constants
Rationalize trends in acid–base of operations strength in relation to molecular structure
Deport out equilibrium calculations for weak acrid–base systems

Nosotros can rank the strengths of acids by the extent to which they ionize in aqueous solution. The reaction of an acid with water is given by the general expression:

\[\ce{HA}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq) \nonumber \]

H2o is the base that reacts with the acid \(\ce{HA}\), \(\ce{A^{−}}\) is the conjugate base of the acid \(\ce{HA}\), and the hydronium ion is the conjugate acid of water. A strong acrid yields 100% (or very nearly so) of \(\ce{H3O+}\) and \(\ce{A^{−}}\) when the acid ionizes in h2o; Effigy \(\PageIndex{ane}\) lists several stiff acids. A weak acid gives minor amounts of \(\ce{H3O+}\) and \(\ce{A^{−}}\).

Figure \(\PageIndex{ane}\): Some of the common strong acids and bases are listed here.
Six Strong Acids		Six Potent Bases
\(\ce{HClO4}\)	perchloric acid	\(\ce{LiOH}\)	lithium hydroxide
\(\ce{HCl}\)	hydrochloric acid	\(\ce{NaOH}\)	sodium hydroxide
\(\ce{HBr}\)	hydrobromic acid	\(\ce{KOH}\)	potassium hydroxide
\(\ce{HI}\)	hydroiodic acrid	\(\ce{Ca(OH)2}\)	calcium hydroxide
\(\ce{HNO3}\)	nitric acid	\(\ce{Sr(OH)2}\)	strontium hydroxide
\(\ce{H2SO4}\)	sulfuric acrid	\(\ce{Ba(OH)2}\)	barium hydroxide

The relative strengths of acids may exist determined by measuring their equilibrium constants in aqueous solutions. In solutions of the aforementioned concentration, stronger acids ionize to a greater extent, and so yield higher concentrations of hydronium ions than do weaker acids. The equilibrium constant for an acid is called the acid-ionization constant, K _a . For the reaction of an acid \(\ce{HA}\):

\[\ce{HA}(aq)+\ce{H2O}(50)⇌\ce{H3O+}(aq)+\ce{A-}(aq) \nonumber \]

we write the equation for the ionization constant as:

\[K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}} \nonumber \]

where the concentrations are those at equilibrium. As noted in the department on equilibrium constants, although water is a reactant in the reaction, it is the solvent as well, so its activity has a value of one, which does not alter the value of \(K_a\).

Annotation

Information technology is a common mistake to claim that the molar concentration of the solvent is in some manner involved in the equilibrium law. This error is a result of a misunderstanding of solution thermodynamics. For instance, it is ofttimes claimed that K_a = K_eq[H_twoO] for aqueous solutions. This equation is incorrect because information technology is an erroneous interpretation of the right equation Chiliad_a = 1000_eq(\(\textit{a}_{H_2O}\)). Because \(\textit{a}_{H_2O}\) = 1 for a dilute solution, One thousand_a = K_eq(1), or Chiliad_a = K_eq.

The larger the \(K_a\) of an acrid, the larger the concentration of \(\ce{H3O+}\) and \(\ce{A^{−}}\) relative to the concentration of the nonionized acid, \(\ce{HA}\). Thus a stronger acid has a larger ionization constant than does a weaker acrid. The ionization constants increment as the strengths of the acids increase.

The following data on acid-ionization constants indicate the order of acid force: \(\ce{CH3CO2H} < \ce{HNO2} < \ce{HSO4-}\)

\[ \brainstorm{aligned} \ce{CH3CO2H}(aq) + \ce{Water}(l) &⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \quad &K_\ce{a}=1.8×10^{−5} \\[4pt] \ce{HNO2}(aq)+\ce{Water}(l) &⇌\ce{H3O+}(aq)+\ce{NO2-}(aq) &K_\ce{a}=iv.6×10^{-4} \\[4pt] \ce{HSO4-}(aq)+\ce{Water}(l) &⇌\ce{H3O+}(aq)+\ce{SO4^two-}(aq) & K_\ce{a}=ane.two×ten^{−ii} \end{aligned} \nonumber \]

Another measure of the force of an acrid is its percent ionization. The percent ionization of a weak acrid is the ratio of the concentration of the ionized acid to the initial acid concentration, times 100:

\[\% \:\ce{ionization}=\ce{\dfrac{[H3O+]_{eq}}{[HA]_0}}×100\% \label{PercentIon} \]

Because the ratio includes the initial concentration, the percent ionization for a solution of a given weak acid varies depending on the original concentration of the acrid, and actually decreases with increasing acid concentration.

Example \(\PageIndex{ane}\): Calculation of Per centum Ionization from pH

Calculate the per centum ionization of a 0.125-M solution of nitrous acid (a weak acid), with a pH of two.09.

Solution

The percent ionization for an acid is:

\[\ce{\dfrac{[H3O+]_{eq}}{[HNO2]_0}}×100 \nonumber \]

The chemic equation for the dissociation of the nitrous acrid is:

\[\ce{HNO2}(aq)+\ce{H2o}(l)⇌\ce{NO2-}(aq)+\ce{H3O+}(aq). \nonumber \]

Since \(10^{−pH} = \ce{[H3O+]}\), we find that \(10^{−2.09} = eight.1 \times 10^{−three}\, M\), and so that percent ionization (Equation \ref{PercentIon}) is:

\[\dfrac{eight.one×10^{−three}}{0.125}×100=6.5\% \nonumber \]

Call back, the logarithm 2.09 indicates a hydronium ion concentration with only 2 meaning figures.

Exercise \(\PageIndex{ane}\)

Summate the percent ionization of a 0.10 1000 solution of acetic acid with a pH of two.89.

Reply: one.iii% ionized

We tin rank the strengths of bases by their tendency to course hydroxide ions in aqueous solution. The reaction of a Brønsted-Lowry base with h2o is given past:

\[\ce{B}(aq)+\ce{H2O}(l)⇌\ce{HB+}(aq)+\ce{OH-}(aq) \nonumber \]

Water is the acrid that reacts with the base, \(\ce{HB^{+}}\) is the conjugate acid of the base \(\ce{B}\), and the hydroxide ion is the cohabit base of h2o. A strong base of operations yields 100% (or very well-nigh then) of OH⁻ and HB⁺ when information technology reacts with water; Figure \(\PageIndex{1}\) lists several strong bases. A weak base yields a pocket-sized proportion of hydroxide ions. Soluble ionic hydroxides such every bit NaOH are considered strong bases because they dissociate completely when dissolved in water.

Equally we did with acids, nosotros tin measure the relative strengths of bases by measuring their base-ionization abiding (Chiliad _b) in aqueous solutions. In solutions of the same concentration, stronger bases ionize to a greater extent, and so yield higher hydroxide ion concentrations than practice weaker bases. A stronger base has a larger ionization constant than does a weaker base. For the reaction of a base, \(\ce{B}\):

\[\ce{B}(aq)+\ce{Water}(l)⇌\ce{HB+}(aq)+\ce{OH-}(aq), \nonumber \]

we write the equation for the ionization constant as:

\[K_\ce{b}=\ce{\dfrac{[HB+][OH- ]}{[B]}} \nonumber \]

where the concentrations are those at equilibrium. Again, we do non see water in the equation because water is the solvent and has an action of 1. The chemical reactions and ionization constants of the iii bases shown are:

\[ \begin{aligned} \ce{NO2-}(aq)+\ce{Water}(50) &⇌\ce{HNO2}(aq)+\ce{OH-}(aq) \quad &K_\ce{b}=2.17×10^{−11} \\[4pt] \ce{CH3CO2-}(aq)+\ce{H2O}(l) &⇌\ce{CH3CO2H}(aq)+\ce{OH-}(aq) &K_\ce{b}=five.six×10^{−10} \\[4pt] \ce{NH3}(aq)+\ce{H2O}(fifty) &⇌\ce{NH4+}(aq)+\ce{OH-}(aq) &K_\ce{b}=one.8×x^{−v} \end{aligned} \nonumber \]

A tabular array of ionization constants of weak bases appears in Tabular array E2. As with acids, percent ionization tin can exist measured for basic solutions, but will vary depending on the base ionization constant and the initial concentration of the solution.

Consider the ionization reactions for a conjugate acid-base pair, \(\ce{HA − A^{−}}\):

\[\ce{HA}(aq)+\ce{H2o}(l)⇌\ce{H3O+}(aq)+\ce{A-}(aq) \nonumber \]

with \(K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\).

\[\ce{A-}(aq)+\ce{Water}(l)⇌\ce{OH-}(aq)+\ce{HA}(aq) \nonumber \]

with \(K_\ce{b}=\ce{\dfrac{[HA][OH]}{[A- ]}}\).

Adding these two chemical equations yields the equation for the autoionization for water:

\[\begin{marshal*} \cancel{\ce{HA}(aq)}+\ce{H2o}(50)+\abolish{\ce{A-}(aq)}+\ce{Water}(l) &⇌ \ce{H3O+}(aq)+\cancel{\ce{A-}(aq)}+\ce{OH-}(aq)+\cancel{\ce{HA}(aq)} \\[4pt] \ce{2H2O}(l) &⇌\ce{H3O+}(aq)+\ce{OH-}(aq) \end{marshal*} \nonumber \]

As shown in the previous affiliate on equilibrium, the \(K\) expression for a chemical equation derived from adding 2 or more other equations is the mathematical product of the other equations' \(K\) expressions. Multiplying the mass-action expressions together and cancelling common terms, we come across that:

\[K_\ce{a}×K_\ce{b}=\ce{\dfrac{[H3O+][A- ]}{[HA]}×\dfrac{[HA][OH- ]}{[A- ]}}=\ce{[H3O+][OH- ]}=K_\ce{w} \nonumber \]

For example, the acrid ionization constant of acetic acid (CH₃COOH) is i.8 × 10⁻⁵, and the base ionization constant of its cohabit base, acetate ion (\(\ce{CH3COO-}\)), is five.vi × 10⁻¹⁰. The product of these two constants is indeed equal to \(K_w\):

\[K_\ce{a}×K_\ce{b}=(1.8×10^{−5})×(5.6×10^{−x})=1.0×ten^{−fourteen}=K_\ce{westward} \nonumber \]

The extent to which an acrid, \(\ce{HA}\), donates protons to h2o molecules depends on the forcefulness of the cohabit base, \(\ce{A^{−}}\), of the acid. If \(\ce{A^{−}}\) is a strong base, any protons that are donated to water molecules are recaptured by \(\ce{A^{−}}\). Thus in that location is relatively little \(\ce{A^{−}}\) and \(\ce{H3O+}\) in solution, and the acid, \(\ce{HA}\), is weak. If \(\ce{A^{−}}\) is a weak base, water binds the protons more strongly, and the solution contains primarily \(\ce{A^{−}}\) and \(\ce{H3O^{+}}\)—the acrid is strong. Potent acids grade very weak conjugate bases, and weak acids class stronger conjugate bases (Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): This diagram shows the relative strengths of conjugate acid-base pairs, as indicated by their ionization constants in aqueous solution.

Figure \(\PageIndex{three}\) lists a serial of acids and bases in order of the decreasing strengths of the acids and the respective increasing strengths of the bases. The acid and base in a given row are conjugate to each other.

The beginning six acids in Figure \(\PageIndex{three}\) are the most common strong acids. These acids are completely dissociated in aqueous solution. The conjugate bases of these acids are weaker bases than water. When one of these acids dissolves in h2o, their protons are completely transferred to h2o, the stronger base.

Those acids that prevarication betwixt the hydronium ion and water in Figure \(\PageIndex{iii}\) form conjugate bases that can compete with water for possession of a proton. Both hydronium ions and nonionized acrid molecules are present in equilibrium in a solution of one of these acids. Compounds that are weaker acids than water (those plant below water in the column of acids) in Figure \(\PageIndex{three}\) exhibit no observable acidic beliefs when dissolved in h2o. Their conjugate bases are stronger than the hydroxide ion, and if any conjugate base were formed, it would react with h2o to re-course the acid.

Figure \(\PageIndex{3}\): The chart shows the relative strengths of cohabit acrid-base of operations pairs.

The extent to which a base forms hydroxide ion in aqueous solution depends on the forcefulness of the base relative to that of the hydroxide ion, as shown in the last column in Figure \(\PageIndex{3}\). A strong base of operations, such as i of those lying beneath hydroxide ion, accepts protons from water to yield 100% of the conjugate acrid and hydroxide ion. Those bases lying between water and hydroxide ion take protons from h2o, but a mixture of the hydroxide ion and the base results. Bases that are weaker than h2o (those that lie above water in the cavalcade of bases) show no observable bones beliefs in aqueous solution.

Case \(\PageIndex{two}\): The Product K _a × K_b = M _{due west}

Use the \(K_b\) for the nitrite ion, \(\ce{NO2-}\), to calculate the \(K_a\) for its cohabit acid.

Solution

Yard _b for \(\ce{NO2-}\) is given in this section as 2.17 × ten⁻¹¹. The conjugate acid of \(\ce{NO2-}\) is HNO₂; K _a for HNO_ii can be calculated using the relationship:

\[K_\ce{a}×K_\ce{b}=1.0×10^{−xiv}=K_\ce{west} \nonumber \]

Solving for M _a, we go:

\[\begin{align*} K_\ce{a} &=\dfrac{K_\ce{westward}}{K_\ce{b}} \\[4pt] &=\dfrac{i.0×x^{−14}}{two.17×10^{−11}} \\[4pt] &=4.6×10^{−four} \end{marshal*} \nonumber \]

This answer can be verified by finding the K _a for HNO₂ in Table E1

Exercise \(\PageIndex{2}\)

Nosotros can make up one's mind the relative acid strengths of \(\ce{NH4+}\) and \(\ce{HCN}\) past comparing their ionization constants. The ionization constant of \(\ce{HCN}\) is given in Tabular array E1 as 4.nine × 10^−ten. The ionization abiding of \(\ce{NH4+}\) is non listed, but the ionization constant of its cohabit base, \(\ce{NH3}\), is listed every bit 1.8 × 10^−five. Determine the ionization constant of \(\ce{NH4+}\), and decide which is the stronger acid, \(\ce{HCN}\) or \(\ce{NH4+}\).

Reply: \(\ce{NH4+}\) is the slightly stronger acrid (K _a for \(\ce{NH4+}\) = 5.6 × 10^−x).

The Ionization of Weak Acids and Weak Bases

Many acids and bases are weak; that is, they do not ionize fully in aqueous solution. A solution of a weak acid in water is a mixture of the nonionized acid, hydronium ion, and the conjugate base of operations of the acid, with the nonionized acid nowadays in the greatest concentration. Thus, a weak acid increases the hydronium ion concentration in an aqueous solution (but non as much as the same amount of a potent acid).

Acetic acrid (\(\ce{CH3CO2H}\)) is a weak acid. When we add together acetic acrid to h2o, it ionizes to a small extent according to the equation:

\[\ce{CH3CO2H}(aq)+\ce{H2o}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \nonumber \]

giving an equilibrium mixture with most of the acid present in the nonionized (molecular) form. This equilibrium, like other equilibria, is dynamic; acetic acrid molecules donate hydrogen ions to h2o molecules and course hydronium ions and acetate ions at the same rate that hydronium ions donate hydrogen ions to acetate ions to reform acetic acid molecules and water molecules. We tin can tell past measuring the pH of an aqueous solution of known concentration that only a fraction of the weak acid is ionized at any moment (Effigy \(\PageIndex{4}\)). The remaining weak acrid is nowadays in the nonionized form.

For acetic acid, at equilibrium:

\[K_\ce{a}=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}}=ane.8 \times x^{−5} \nonumber \]

Figure \(\PageIndex{4}\): pH paper indicates that a 0.50-1000 solution of \(\ce{HCl}\) (chalice on left) has a pH of 1. The acrid is fully ionized and \(\ce{[H3O+]}\) = 0.1 Yard. A 0.1-M solution of CH₃CO_iiH (beaker on right) has a pH of iii ( \(\ce{[H3O+]}\) = 0.001 Thousand) because the weak acrid CH₃CO_twoH is only partially ionized. In this solution, \(\ce{[H3O+]} < [\ce{CH3CO2H}]\). (credit: modification of work by Sahar Atwa)

Tabular array \(\PageIndex{i}\): Ionization Constants of Some Weak Acids
Ionization Reaction	K _a at 25 °C
\(\ce{HSO4- + H2O ⇌ H3O+ + SO4^ii-}\)	ane.2 × ten⁻²
\(\ce{HF + Water ⇌ H3O+ + F-}\)	3.v × ten⁻⁴
\(\ce{HNO2 + H2O ⇌ H3O+ + NO2-}\)	iv.6 × x⁻⁴
\(\ce{HNCO + Water ⇌ H3O+ + NCO-}\)	2 × 10⁻⁴
\(\ce{HCO2H + H2O ⇌ H3O+ + HCO2-}\)	one.8 × 10⁻⁴
\(\ce{CH3CO2H + H2o ⇌ H3O+ + CH3CO2-}\)	1.viii × 10⁻⁵
\(\ce{HCIO + H2o ⇌ H3O+ + CIO-}\)	two.9 × x⁻⁸
\(\ce{HBrO + H2o ⇌ H3O+ + BrO-}\)	2.8 × x^−nine
\(\ce{HCN + Water ⇌ H3O+ + CN-}\)	4.ix × 10⁻¹⁰

Tabular array \(\PageIndex{1}\) gives the ionization constants for several weak acids; additional ionization constants can be plant in Table E1.

At equilibrium, a solution of a weak base in water is a mixture of the nonionized base, the conjugate acrid of the weak base, and hydroxide ion with the nonionized base of operations nowadays in the greatest concentration. Thus, a weak base increases the hydroxide ion concentration in an aqueous solution (but non as much equally the aforementioned corporeality of a strong base).

For instance, a solution of the weak base trimethylamine, (CH₃)_iiiN, in water reacts according to the equation:

\[\ce{(CH3)3N}(aq)+\ce{H2o}(l)⇌\ce{(CH3)3NH+}(aq)+\ce{OH-}(aq) \nonumber \]

This gives an equilibrium mixture with near of the base present as the nonionized amine. This equilibrium is coordinating to that described for weak acids.

We can confirm past measuring the pH of an aqueous solution of a weak base of known concentration that but a fraction of the base of operations reacts with h2o (Figure 14.4.5). The remaining weak base is nowadays as the unreacted form. The equilibrium constant for the ionization of a weak base, \(K_b\), is called the ionization constant of the weak base, and is equal to the reaction quotient when the reaction is at equilibrium. For trimethylamine, at equilibrium:

\[K_\ce{b}=\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}} \nonumber \]

alt — Figure \(\PageIndex{five}\): pH paper indicates that a 0.1-1000 solution of NH₃ (left) is weakly basic. The solution has a pOH of three ([OH⁻] = 0.001 Thousand) because the weak base of operations NH₃ only partially reacts with water. A 0.1-Thou solution of NaOH (correct) has a pOH of 1 because NaOH is a strong base (credit: modification of work past Sahar Atwa).

The ionization constants of several weak bases are given in Table \(\PageIndex{2}\) and Tabular array E2.

Table \(\PageIndex{2}\): Ionization Constants of Some Weak Bases
Ionization Reaction	K_b at 25 °C
\(\ce{(CH3)2NH + H2o ⇌ (CH3)2NH2+ + OH-}\)	5.9 × 10^−four
\(\ce{CH3NH2 + H2O ⇌ CH3NH3+ + OH-}\)	4.4 × 10⁻⁴
\(\ce{(CH3)3N + Water ⇌ (CH3)3NH+ + OH-}\)	six.3 × 10⁻⁵
\(\ce{NH3 + H2O ⇌ NH4+ + OH-}\)	1.8 × ten⁻⁵
\(\ce{C6H5NH2 + H2O ⇌ C6N5NH3+ + OH-}\)	4.three × 10⁻¹⁰

Example \(\PageIndex{3}\): Decision of G _a from Equilibrium Concentrations

Acetic acid is the primary ingredient in vinegar; that's why it tastes sour. At equilibrium, a solution contains [CH₃CO₂H] = 0.0787 1000 and \(\ce{[H3O+]}=\ce{[CH3CO2- ]}=0.00118\:M\). What is the value of \(K_a\) for acetic acrid?

alt — Vinegar is a solution of acetic acid, a weak acrid. (credit: modification of work by "HomeSpot HQ"/Flickr)

Solution

We are asked to calculate an equilibrium constant from equilibrium concentrations. At equilibrium, the value of the equilibrium abiding is equal to the reaction quotient for the reaction:

\[\ce{CH3CO2H}(aq)+\ce{H2O}(50)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \nonumber \]

\[\begin{align*} K_\ce{a} &=\ce{\dfrac{[H3O+][CH3CO2- ]}{[CH3CO2H]}} \\[4pt] &=\dfrac{(0.00118)(0.00118)}{0.0787} \\[4pt] &=1.77×10^{−5} \end{marshal*} \nonumber \]

Do \(\PageIndex{iii}\)

What is the equilibrium constant for the ionization of the \(\ce{HSO4-}\) ion, the weak acid used in some household cleansers:

\[\ce{HSO4-}(aq)+\ce{Water}(l)⇌\ce{H3O+}(aq)+\ce{SO4^two-}(aq) \nonumber \]

In ane mixture of NaHSO₄ and Na₂Then₄ at equilibrium, \(\ce{[H3O+]}\) = 0.027 M; \(\ce{[HSO4- ]}=0.29\:G\); and \(\ce{[SO4^2- ]}=0.13\:K\).

Answer: \(K_a\) for \(\ce{HSO_4^-}= 1.2 ×\times 10^{−2}\)

Case \(\PageIndex{4}\): Decision of Thousand _b from Equilibrium Concentrations

Caffeine, C₈H₁₀N₄O₂ is a weak base of operations. What is the value of Grand _b for caffeine if a solution at equilibrium has [C₈H₁₀Due north₄O_two] = 0.050 One thousand, \(\ce{[C8H10N4O2H+]}\) = 5.0 × 10⁻³ M, and [OH⁻] = two.five × x⁻³ Chiliad?

Solution

At equilibrium, the value of the equilibrium abiding is equal to the reaction quotient for the reaction:

\[\ce{C8H10N4O2}(aq)+\ce{H2o}(l)⇌\ce{C8H10N4O2H+}(aq)+\ce{OH-}(aq) \nonumber \]

\[K_\ce{b}=\ce{\dfrac{[C8H10N4O2H+][OH- ]}{[C8H10N4O2]}}=\dfrac{(v.0×10^{−3})(ii.v×x^{−3})}{0.050}=2.5×x^{−four} \nonumber \]

Exercise \(\PageIndex{4}\)

What is the equilibrium abiding for the ionization of the \(\ce{HPO4^2-}\) ion, a weak base:

\[\ce{HPO4^2-}(aq)+\ce{Water}(l)⇌\ce{H2PO4-}(aq)+\ce{OH-}(aq) \nonumber \]

In a solution containing a mixture of \(\ce{NaH2PO4}\) and \(\ce{Na2HPO4}\) at equilibrium with:

\([\ce{OH^{−}}] = one.3 × ten^{−six} 1000\)
\(\ce{[H2PO4^{-}]=0.042\:Thousand}\) and
\(\ce{[HPO4^{2-}]=0.341\:M}\).

Answer: K _b for \(\ce{HPO4^2-}=1.6×10^{−7} \)

Instance \(\PageIndex{v}\): Determination of G _a or G _b from pH

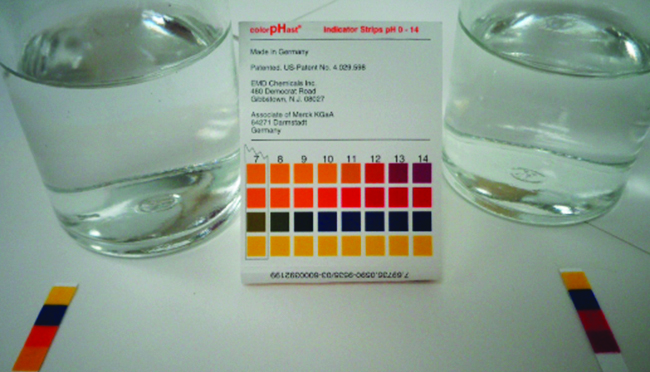
The pH of a 0.0516-M solution of nitrous acid, \(\ce{HNO2}\), is ii.34. What is its \(K_a\)?

\[\ce{HNO2}(aq)+\ce{H2o}(50)⇌\ce{H3O+}(aq)+\ce{NO2-}(aq) \nonumber \]

Solution

We determine an equilibrium abiding starting with the initial concentrations of HNO₂, \(\ce{H3O+}\), and \(\ce{NO2-}\) as well equally ane of the last concentrations, the concentration of hydronium ion at equilibrium. (Call back that pH is only another style to express the concentration of hydronium ion.)

Nosotros can solve this problem with the following steps in which x is a change in concentration of a species in the reaction:

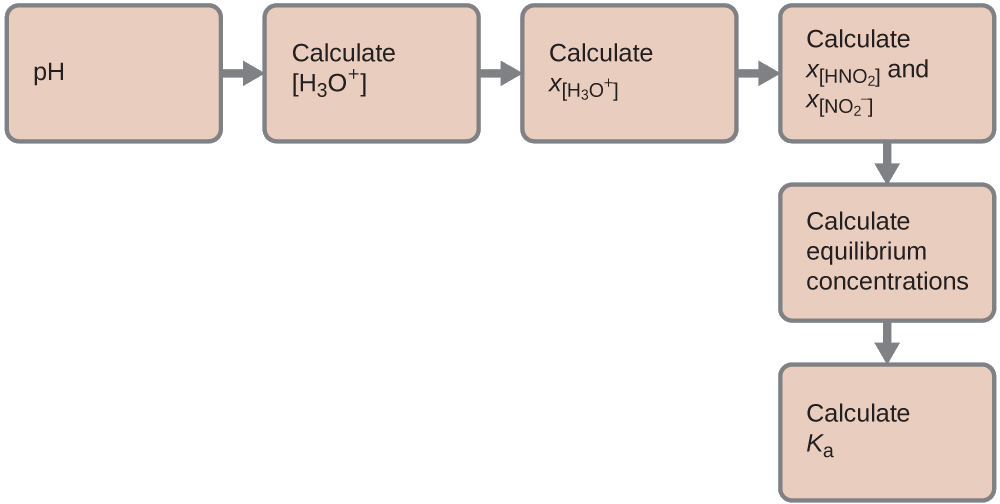
Example 14.3.5.png

Nosotros can summarize the various concentrations and changes as shown hither. Because water is the solvent, it has a fixed activeness equal to 1. Whatever minor amount of water produced or used up during the reaction will not change h2o's office as the solvent, and then the value of its activity remains equal to 1 throughout the reaction.

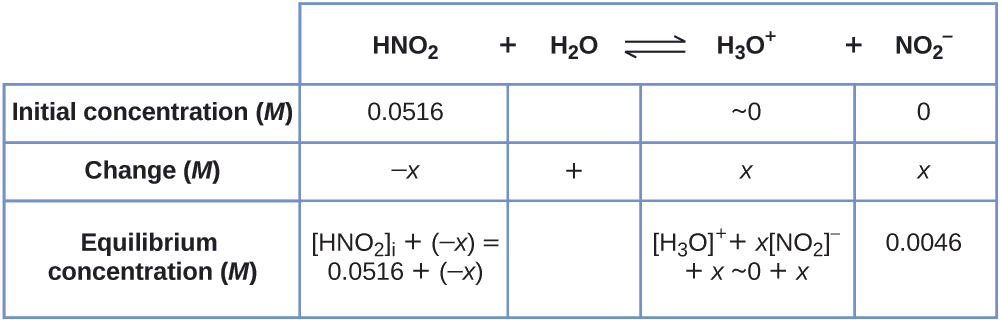
Example 14.3.5B.png

To go the various values in the Water ice (Initial, Change, Equilibrium) table, we first calculate \(\ce{[H3O+]}\), the equilibrium concentration of \(\ce{H3O+}\), from the pH:

\[\ce{[H3O+]}=10^{−2.34}=0.0046\:M \nonumber \]

The alter in concentration of \(\ce{H3O+}\), \(x_{\ce{[H3O+]}}\), is the departure betwixt the equilibrium concentration of H₃O⁺, which nosotros determined from the pH, and the initial concentration, \(\mathrm{[H_3O^+]_i}\). The initial concentration of \(\ce{H3O+}\) is its concentration in pure water, which is so much less than the final concentration that we approximate it as nix (~0).

The alter in concentration of \(\ce{NO2-}\) is equal to the change in concentration of \(\ce{[H3O+]}\). For each 1 mol of \(\ce{H3O+}\) that forms, 1 mol of \(\ce{NO2-}\) forms. The equilibrium concentration of HNO₂ is equal to its initial concentration plus the modify in its concentration.

At present we can fill in the ICE tabular array with the concentrations at equilibrium, equally shown here:

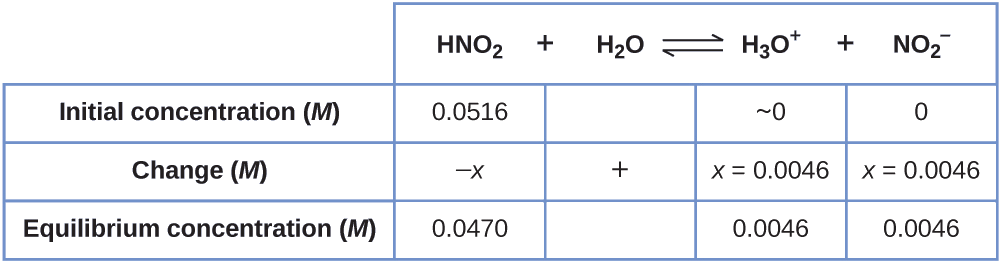
Finally, we calculate the value of the equilibrium abiding using the data in the tabular array:

\[K_\ce{a}=\ce{\dfrac{[H3O+][NO2- ]}{[HNO2]}}=\dfrac{(0.0046)(0.0046)}{(0.0470)}=4.5×10^{−4} \nonumber \]

Exercise \(\PageIndex{5}\)

The pH of a solution of household ammonia, a 0.950-Grand solution of NH₃ _, is 11.612. What is K _b for NH₃.

Reply: \(K_b = one.8 × 10^{−5}\)

Example \(\PageIndex{6}\): Equilibrium Concentrations in a Solution of a Weak Acid

Formic acid, HCO₂H, is the irritant that causes the body's reaction to ant stings.

A photograph is shown of a large black ant on the end of a human finger. — The pain of an ant'due south sting is caused past formic acid. (credit: John Tann)

What is the concentration of hydronium ion and the pH in a 0.534-M solution of formic acid?

\[\ce{HCO2H}(aq)+\ce{H2o}(l)⇌\ce{H3O+}(aq)+\ce{HCO2-}(aq) \hspace{20px} K_\ce{a}=1.eight×10^{−4} \nonumber \]

Solution

one. Determine x and equilibrium concentrations. The equilibrium expression is:

\[\ce{HCO2H}(aq)+\ce{H2O}(50)⇌\ce{H3O+}(aq)+\ce{HCO2-}(aq) \nonumber \]

Considering h2o is the solvent, information technology has a fixed activity equal to ane. Any small corporeality of water produced or used up during the reaction will non modify water'south role as the solvent, then the value of its activity remains equal to i throughout the reaction then we practice not need to consider information technology when setting upwards the ICE table.

The table shows initial concentrations (concentrations before the acrid ionizes), changes in concentration, and equilibrium concentrations follows (the information given in the problem appear in color):

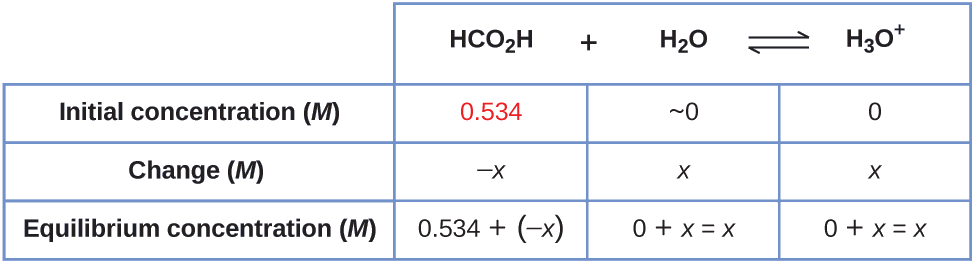
Example 14.3.6.png

ii. Solve for \(ten\) and the equilibrium concentrations. At equilibrium:

\[\begin{align*} K_\ce{a} &=ane.viii×10^{−4}=\ce{\dfrac{[H3O+][HCO2- ]}{[HCO2H]}} \\[4pt] &=\dfrac{(x)(x)}{0.534−x}=ane.8×x^{−4} \end{marshal*} \nonumber \]

Now solve for \(x\). Considering the initial concentration of acid is reasonably large and \(K_a\) is very small, we assume that \(x << 0.534\), which permits us to simplify the denominator term every bit \((0.534 − x) = 0.534\). This gives:

\[K_\ce{a}=1.8×ten^{−4}=\dfrac{x^{2}}{0.534} \nonumber \]

Solve for \(ten\) as follows:

\[\begin{marshal*} 10^ii &=0.534×(1.eight×10^{−4}) \\[4pt] &=9.half-dozen×10^{−v} \\[4pt] x &=\sqrt{ix.6×10^{−v}} \\[4pt] &=9.8×10^{−3} \end{align*} \nonumber \]

To check the supposition that \(x\) is small compared to 0.534, nosotros calculate:

\[\begin{align*} \dfrac{x}{0.534} &=\dfrac{nine.8×10^{−3}}{0.534} \\[4pt] &=1.8×10^{−two} \, \textrm{(ane.eight% of 0.534)} \end{marshal*} \nonumber \]

\(ten\) is less than 5% of the initial concentration; the assumption is valid.

We notice the equilibrium concentration of hydronium ion in this formic acrid solution from its initial concentration and the change in that concentration as indicated in the last line of the tabular array:

\[\begin{align*} \ce{[H3O+]} &=~0+10=0+9.8×ten^{−three}\:K. \\[4pt] &=ix.8×10^{−3}\:M \end{align*} \nonumber \]

The pH of the solution tin be establish by taking the negative log of the \(\ce{[H3O+]}\), so:

\[pH = −\log(9.8×10^{−3})=2.01 \nonumber \]

Exercise \(\PageIndex{6}\): acerb acid

Only a small fraction of a weak acid ionizes in aqueous solution. What is the pct ionization of acetic acrid in a 0.100-1000 solution of acetic acrid, CH₃CO₂H?

\[\ce{CH3CO2H}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{CH3CO2-}(aq) \hspace{20px} K_\ce{a}=1.8×10^{−five} \nonumber \]

Hint: Determine \(\ce{[CH3CO2- ]}\) at equilibrium.) Recollect that the percent ionization is the fraction of acetic acid that is ionized × 100, or \(\ce{\dfrac{[CH3CO2- ]}{[CH3CO2H]_{initial}}}×100\).

Reply: percent ionization = one.3%

The post-obit example shows that the concentration of products produced by the ionization of a weak base can exist determined by the same serial of steps used with a weak acid.

Case \(\PageIndex{7}\): Equilibrium Concentrations in a Solution of a Weak Base

Observe the concentration of hydroxide ion in a 0.25-M solution of trimethylamine, a weak base:

\[\ce{(CH3)3N}(aq)+\ce{H2o}(l)⇌\ce{(CH3)3NH+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=half-dozen.three×10^{−v} \nonumber \]

Solution This trouble requires that we calculate an equilibrium concentration by determining concentration changes every bit the ionization of a base goes to equilibrium. The solution is approached in the same fashion every bit that for the ionization of formic acid in Example \(\PageIndex{6}\). The reactants and products will be different and the numbers will be different, but the logic will be the aforementioned:

Example 14.3.7A.png

ane. Determine x and equilibrium concentrations. The table shows the changes and concentrations:

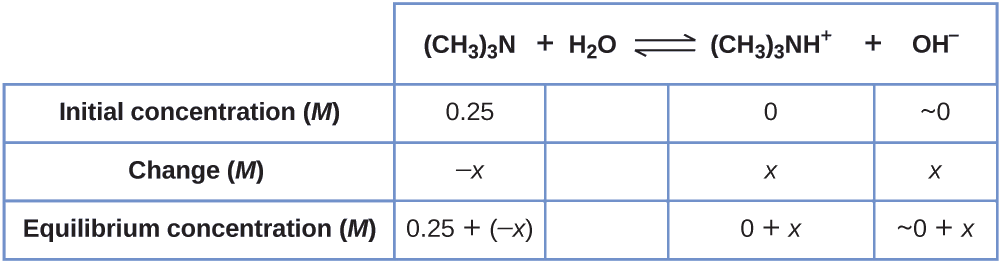
Example 14.3.7B.png

2. Solve for \(x\) and the equilibrium concentrations. At equilibrium:

\[K_\ce{b}=\ce{\dfrac{[(CH3)3NH+][OH- ]}{[(CH3)3N]}}=\dfrac{(x)(x)}{0.25−x=}6.3×ten^{−5} \nonumber \]

If nosotros assume that x is pocket-sized relative to 0.25, then we tin supervene upon (0.25 − x) in the preceding equation with 0.25. Solving the simplified equation gives:

\[x=iv.0×10^{−3} \nonumber \]

This change is less than 5% of the initial concentration (0.25), and then the assumption is justified.

Recollect that, for this ciphering, \(x\) is equal to the equilibrium concentration of hydroxide ion in the solution (see earlier tabulation):

\[\begin{align*} (\ce{[OH- ]}=~0+ten=10=iv.0×10^{−3}\:M \\[4pt] &=4.0×ten^{−iii}\:M \cease{align*} \nonumber \]

Then calculate pOH equally follows:

\[\ce{pOH}=−\log(4.iii×10^{−3})=2.40 \nonumber \]

Using the relation introduced in the previous section of this chapter:

\[\mathrm{pH + pOH=p\mathit{Yard}_w=14.00}\nonumber \]

permits the computation of pH:

\[\mathrm{pH=14.00−pOH=14.00−2.37=eleven.60} \nonumber \]

Bank check the work. A check of our arithmetics shows that \(K_b = 6.three \times 10^{−v}\).

Exercise \(\PageIndex{seven}\)

Evidence that the calculation in Step 2 of this case gives an x of 4.iii × 10⁻³ and the calculation in Footstep iii shows K _b = 6.iii × 10⁻⁵.
Discover the concentration of hydroxide ion in a 0.0325-Thou solution of ammonia, a weak base of operations with a K _b of 1.76 × 10⁻⁵. Calculate the percentage ionization of ammonia, the fraction ionized × 100, or \(\ce{\dfrac{[NH4+]}{[NH3]}}×100 \%\)

Respond a: \(7.56 × 10^{−4}\, M\), 2.33%
Answer b: 2.33%

Some weak acids and weak bases ionize to such an extent that the simplifying supposition that x is small relative to the initial concentration of the acid or base is inappropriate. As we solve for the equilibrium concentrations in such cases, nosotros will see that we cannot neglect the change in the initial concentration of the acid or base of operations, and we must solve the equilibrium equations by using the quadratic equation.

Example \(\PageIndex{eight}\): Equilibrium Concentrations in a Solution of a Weak Acid

Sodium bisulfate, NaHSO₄, is used in some household cleansers because it contains the \(\ce{HSO4-}\) ion, a weak acrid. What is the pH of a 0.50-G solution of \(\ce{HSO4-}\)?

\[\ce{HSO4-}(aq)+\ce{H2O}(l)⇌\ce{H3O+}(aq)+\ce{SO4^ii-}(aq) \hspace{20px} K_\ce{a}=1.2×10^{−2} \nonumber \]

Solution

Nosotros need to decide the equilibrium concentration of the hydronium ion that results from the ionization of \(\ce{HSO4-}\) so that nosotros tin can employ \(\ce{[H3O+]}\) to make up one's mind the pH. As in the previous examples, we tin can approach the solution by the following steps:

Example 14.3.8A.png

1. Make up one's mind \(10\) and equilibrium concentrations. This tabular array shows the changes and concentrations:

Example 14.3.8B.png

ii. Solve for \(x\) and the concentrations.

Equally nosotros begin solving for \(10\), we will discover this is more complicated than in previous examples. Equally we discuss these complications nosotros should not lose track of the fact that it is however the purpose of this footstep to determine the value of \(x\).

At equilibrium:

\[K_\ce{a}=ane.ii×10^{−2}=\ce{\dfrac{[H3O+][SO4^2- ]}{[HSO4- ]}}=\dfrac{(10)(x)}{0.fifty−10} \nonumber \]

If nosotros assume that x is minor and approximate (0.50 − ten) as 0.50, nosotros find:

\[x=vii.7×10^{−2} \nonumber \]

When we check the assumption, we confirm:

\[\dfrac{x}{\mathrm{[HSO_4^- ]_i}} \overset{?}{\le} 0.05 \nonumber \]

which for this system is

\[\dfrac{ten}{0.50}=\dfrac{7.7×ten^{−two}}{0.fifty}=0.xv(15\%) \nonumber \]

The value of \(10\) is not less than 5% of 0.50, so the assumption is not valid. Nosotros demand the quadratic formula to find \(x\).

The equation:

\[K_\ce{a}=one.2×x^{−ii}=\dfrac{(x)(ten)}{0.50−x}\nonumber \]

gives

\[half-dozen.0×10^{−3}−1.ii×10^{−2}10=ten^{two+} \nonumber \]

\[10^{2+}+1.2×10^{−2}10−vi.0×10^{−3}=0 \nonumber \]

This equation can be solved using the quadratic formula. For an equation of the form

\[ax^{2+} + bx + c=0, \nonumber \]

\(x\) is given by the quadratic equation:

\[x=\dfrac{−b±\sqrt{b^{2+}−4ac}}{2a} \nonumber \]

In this problem, \(a = 1\), \(b = i.2 × 10^{−three}\), and \(c = −6.0 × 10^{−3}\).

Solving for x gives a negative root (which cannot be correct since concentration cannot be negative) and a positive root:

\[ten=7.2×10^{−ii} \nonumber \]

Now determine the hydronium ion concentration and the pH:

\[\brainstorm{align*} \ce{[H3O+]} &=~0+x=0+7.ii×10^{−2}\:M \\[4pt] &=7.2×10^{−2}\:M \finish{marshal*} \nonumber \]

The pH of this solution is:

\[\mathrm{pH=−log[H_3O^+]=−log7.2×10^{−2}=1.fourteen} \nonumber \]

Practise \(\PageIndex{8}\)

Show that the quadratic formula gives \(x = 7.2 × ten^{−2}\).
Summate the pH in a 0.010-Thousand solution of caffeine, a weak base:

\[\ce{C8H10N4O2}(aq)+\ce{H2o}(50)⇌\ce{C8H10N4O2H+}(aq)+\ce{OH-}(aq) \hspace{20px} K_\ce{b}=2.5×10^{−4} \nonumber \]

Hint: It will be necessary to catechumen [OH⁻] to \(\ce{[H3O+]}\) or pOH to pH toward the terminate of the calculation.

Respond: pH 11.sixteen

The Relative Strengths of Strong Acids and Bases

Strong acids, such as \(\ce{HCl}\), \(\ce{HBr}\), and \(\ce{Hullo}\), all exhibit the same strength in water. The water molecule is such a potent base of operations compared to the conjugate bases Cl⁻, Br⁻, and I⁻ that ionization of these potent acids is essentially complete in aqueous solutions. In solvents less basic than h2o, we find \(\ce{HCl}\), \(\ce{HBr}\), and \(\ce{HI}\) differ markedly in their tendency to requite upward a proton to the solvent. For case, when dissolved in ethanol (a weaker base of operations than h2o), the extent of ionization increases in the order \(\ce{HCl < HBr < Hello}\), and and so \(\ce{Hullo}\) is demonstrated to be the strongest of these acids. The inability to discern differences in force amid potent acids dissolved in water is known as the leveling effect of h2o.

Water also exerts a leveling effect on the strengths of strong bases. For example, the oxide ion, O²⁻, and the amide ion, \(\ce{NH2-}\), are such stiff bases that they react completely with water:

\[\ce{O^2-}(aq)+\ce{H2O}(50)⟶\ce{OH-}(aq)+\ce{OH-}(aq) \nonumber \]

\[\ce{NH2-}(aq)+\ce{H2o}(l)⟶\ce{NH3}(aq)+\ce{OH-}(aq) \nonumber \]

Thus, O²⁻ and \(\ce{NH2-}\) announced to have the same base strength in water; they both requite a 100% yield of hydroxide ion.

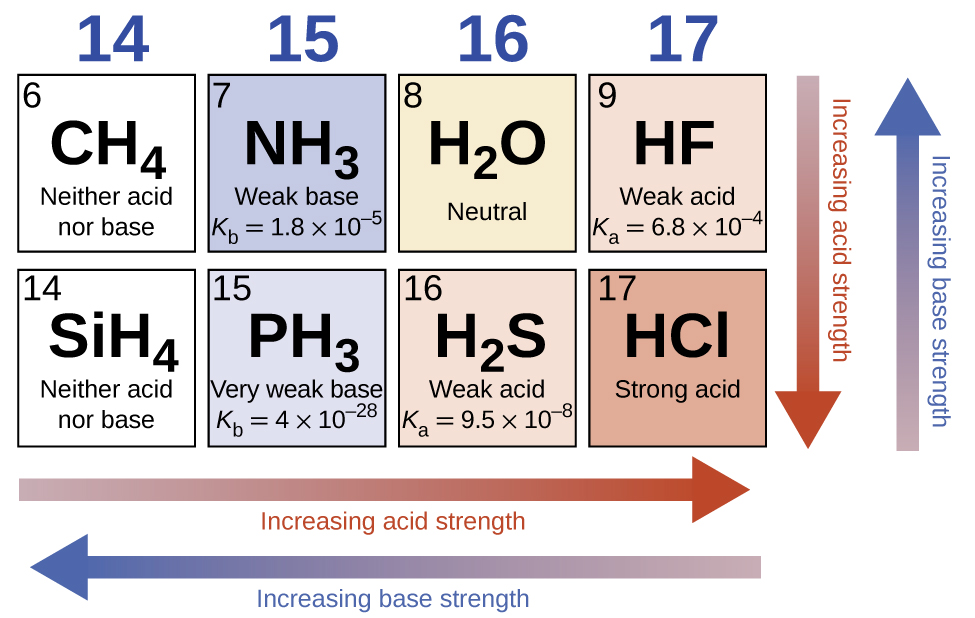
In the absence of any leveling consequence, the acid forcefulness of binary compounds of hydrogen with nonmetals (A) increases equally the H-A bond force decreases down a group in the periodic table. For grouping 17, the order of increasing acerbity is \(\ce{HF < HCl < HBr < HI}\). As well, for group 16, the order of increasing acid strength is H_twoO < H_twoS < H_twoSe < H_iiTe. Across a row in the periodic table, the acid forcefulness of binary hydrogen compounds increases with increasing electronegativity of the nonmetal atom considering the polarity of the H-A bond increases. Thus, the club of increasing acidity (for removal of one proton) beyond the second row is \(\ce{CH4 < NH3 < H2O < HF}\); across the third row, it is \(\ce{SiH4 < PH3 < H2S < HCl}\) (see Figure \(\PageIndex{6}\)).

Figure \(\PageIndex{6}\): As y'all movement from left to correct and downward the periodic tabular array, the acid strength increases. Every bit you move from right to left and upwards, the base strength increases.

Compounds containing oxygen and one or more hydroxyl (OH) groups can be acidic, bones, or amphoteric, depending on the position in the periodic tabular array of the central atom Due east, the atom bonded to the hydroxyl group. Such compounds have the general formula O_nE(OH)_thou, and include sulfuric acrid, \(\ce{O2S(OH)2}\), sulfurous acid, \(\ce{Os(OH)two}\), nitric acid, \(\ce{O2NOH}\), perchloric acid, \(\ce{O3ClOH}\), aluminum hydroxide, \(\ce{Al(OH)iii}\), calcium hydroxide, \(\ce{Ca(OH)2}\), and potassium hydroxide, \(\ce{KOH}\):

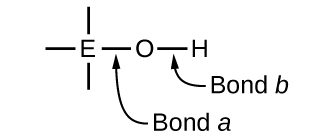
A diagram is shown that includes a primal atom designated with the letter East. Single bonds extend above, below, left, and right of the E. An O atom is bonded to the correct of the E, and an arrow points to the bond labeling it, "Bond a." An H atom is single bonded to the right of the O cantlet. An arrow pointing to this bond connects it to the label, "Bond b."

If the central atom, Due east, has a low electronegativity, its attraction for electrons is low. Lilliputian trend exists for the cardinal atom to form a potent covalent bond with the oxygen atom, and bond a between the element and oxygen is more readily broken than bond b between oxygen and hydrogen. Hence bond a is ionic, hydroxide ions are released to the solution, and the material behaves as a base of operations—this is the instance with Ca(OH)₂ and KOH. Lower electronegativity is feature of the more metal elements; hence, the metallic elements grade ionic hydroxides that are by definition bones compounds.

If, on the other hand, the atom E has a relatively high electronegativity, it strongly attracts the electrons information technology shares with the oxygen atom, making bond a relatively strongly covalent. The oxygen-hydrogen bail, bond b, is thereby weakened because electrons are displaced toward E. Bond b is polar and readily releases hydrogen ions to the solution, and then the fabric behaves equally an acrid. High electronegativities are characteristic of the more nonmetallic elements. Thus, nonmetallic elements form covalent compounds containing acidic −OH groups that are called oxyacids.

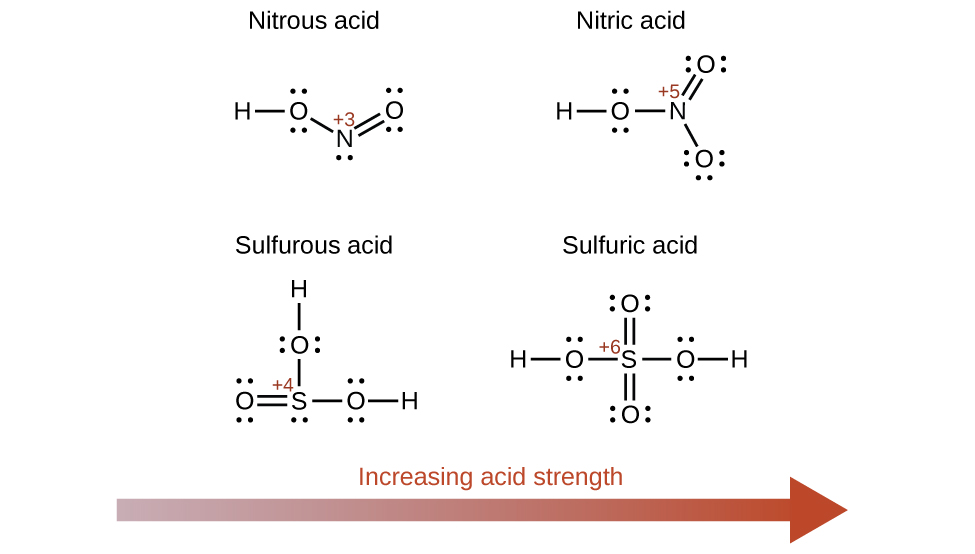
Increasing the oxidation number of the central atom Due east also increases the acidity of an oxyacid because this increases the attraction of East for the electrons it shares with oxygen and thereby weakens the O-H bond. Sulfuric acid, H₂And then_iv, or O_twoS(OH)₂ (with a sulfur oxidation number of +vi), is more than acidic than sulfurous acid, H_iiSo₃, or Bone(OH)₂ (with a sulfur oxidation number of +4). Likewise nitric acid, HNO_iii, or O_two NOH (N oxidation number = +5), is more than acidic than nitrous acid, HNO₂, or ONOH (Due north oxidation number = +3). In each of these pairs, the oxidation number of the central atom is larger for the stronger acid (Figure \(\PageIndex{seven}\)).

Figure \(\PageIndex{seven}\): As the oxidation number of the central atom E increases, the acerbity as well increases.

Hydroxy compounds of elements with intermediate electronegativities and relatively high oxidation numbers (for instance, elements virtually the diagonal line separating the metals from the nonmetals in the periodic table) are usually amphoteric. This means that the hydroxy compounds deed as acids when they react with strong bases and as bases when they react with potent acids. The amphoterism of aluminum hydroxide, which commonly exists equally the hydrate \(\ce{Al(H2O)3(OH)iii}\), is reflected in its solubility in both strong acids and strong bases. In strong bases, the relatively insoluble hydrated aluminum hydroxide, \(\ce{Al(H2O)3(OH)3}\), is converted into the soluble ion, \(\ce{[Al(H2o)2(OH)4]-}\), by reaction with hydroxide ion:

\[[\ce{Al(H2O)three(OH)iii}](aq)+\ce{OH-}(aq)⇌\ce{H2O}(fifty)+\ce{[Al(H2O)ii(OH)4]-}(aq) \nonumber \]

In this reaction, a proton is transferred from one of the aluminum-bound H₂O molecules to a hydroxide ion in solution. The \(\ce{Al(H2O)3(OH)3}\) compound thus acts every bit an acrid under these conditions. On the other mitt, when dissolved in strong acids, information technology is converted to the soluble ion \(\ce{[Al(H2O)6]^iii+}\) by reaction with hydronium ion:

\[\ce{3H3O+}(aq)+\ce{Al(Water)3(OH)3}(aq)⇌\ce{Al(H2O)half dozen^3+}(aq)+\ce{3H2O}(l) \nonumber \]

In this case, protons are transferred from hydronium ions in solution to \(\ce{Al(H2O)three(OH)3}\), and the compound functions as a base.

Summary

The strengths of Brønsted-Lowry acids and bases in aqueous solutions tin can be determined by their acrid or base ionization constants. Stronger acids form weaker conjugate bases, and weaker acids form stronger conjugate bases. Thus potent acids are completely ionized in aqueous solution because their cohabit bases are weaker bases than water. Weak acids are only partially ionized because their cohabit bases are strong enough to compete successfully with h2o for possession of protons. Strong bases react with water to quantitatively form hydroxide ions. Weak bases give only pocket-sized amounts of hydroxide ion. The strengths of the binary acids increase from left to right across a flow of the periodic table (CH₄ < NH₃ < H₂O < HF), and they increase downwards a group (HF < HCl < HBr < HI). The strengths of oxyacids that incorporate the same central chemical element increase as the oxidation number of the element increases (H₂SO_three < H_iiThen_four). The strengths of oxyacids also increase as the electronegativity of the central chemical element increases [H_twoSeO_iv < H₂Then₄].

Key Equations

\(K_\ce{a}=\ce{\dfrac{[H3O+][A- ]}{[HA]}}\)
\(K_\ce{b}=\ce{\dfrac{[HB+][OH- ]}{[B]}}\)
\(K_a \times K_b = 1.0 \times x^{−14} = K_w \,(\text{at room temperature})\)
\(\textrm{Percent ionization}=\ce{\dfrac{[H3O+]_{eq}}{[HA]_0}}×100\)

Glossary

acrid ionization constant (1000 _a): equilibrium constant for the ionization of a weak acid

base of operations ionization abiding (One thousand _b): equilibrium abiding for the ionization of a weak base

leveling effect of water: any acid stronger than \(\ce{H3O+}\), or whatever base stronger than OH⁻ will react with water to form \(\ce{H3O+}\), or OH⁻, respectively; h2o acts as a base of operations to make all stiff acids appear as stiff, and it acts as an acid to make all strong bases announced equally strong

oxyacid: compound containing a nonmetal and one or more hydroxyl groups

percent ionization: ratio of the concentration of the ionized acid to the initial acid concentration, times 100